Let’s be real: geometry can feel intimidating. You’re staring at a triangular prism, maybe it’s a roof truss, a wedge of cheese, or a tent, and you’re thinking, “How do I even calculate this?” The good news? How to find the volume of a triangular prism is actually straightforward once you break it down into bite-sized pieces. No fancy calculus required. Just basic multiplication and a little patience.
Whether you’re a student tackling homework, a contractor estimating materials, or someone curious about the shapes in your world, this guide will walk you through the process with real-world examples and no unnecessary jargon.
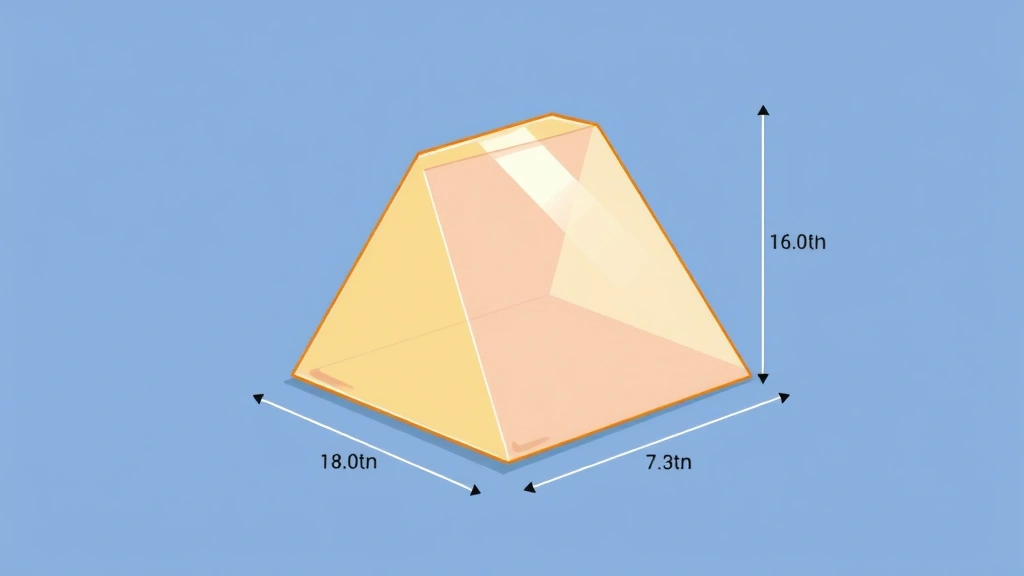
What Is a Triangular Prism?
A triangular prism is a 3D shape with two parallel triangular faces (the bases) and three rectangular faces connecting them. Think of it like a tent: the front and back are triangles, and the roof and floor are rectangles.
Here’s what makes it distinct from other prisms:
- Two identical triangular bases – These are parallel to each other and never touch.
- Three rectangular sides – These connect the edges of the two triangles.
- Straight edges – All edges are straight lines (no curves).
- Uniform cross-section – If you slice it perpendicular to the triangular faces, every slice looks the same.
You’ll see triangular prisms everywhere: roof trusses, toblerone bars, tent structures, and even some architectural designs. Understanding how to find the volume of a triangular prism is useful for anyone working with construction, packaging, or even culinary applications.
Pro Tip: The key to understanding any prism is remembering that volume = base area × height. For a triangular prism, the “base” is the triangular face, and the “height” is the distance between the two triangular faces (not the height of the triangle itself—this trips people up constantly).
The Volume Formula Explained
Here’s the core formula for how to find the volume of a triangular prism:
Volume = (Area of Triangular Base) × (Length/Height of Prism)
Or more formally:
V = (1/2 × b × h) × L
Where:
- b = base of the triangle (one side of the triangular face)
- h = height of the triangle (perpendicular distance from the base to the opposite vertex)
- L = length (or height) of the prism (the distance between the two triangular faces)
This can also be written as:
V = (b × h × L) / 2
The logic is simple: you’re finding the area of one triangular face, then multiplying by how far that triangle extends. It’s like stacking triangles on top of each other.
According to Khan Academy’s geometry resources, understanding the relationship between 2D shapes and 3D volumes is foundational to solid geometry. The triangular prism is one of the most accessible entry points into this concept.
Step-by-Step Calculation
Let’s walk through this with a concrete example. Imagine you have a triangular prism with:
- Triangle base = 5 cm
- Triangle height = 4 cm
- Prism length = 10 cm
Step 1: Find the area of the triangular base.
Use the triangle area formula: Area = 1/2 × base × height
Area = 1/2 × 5 × 4 = 10 cm²
Step 2: Multiply by the prism length.
Volume = 10 cm² × 10 cm = 100 cm³
Done. Your triangular prism has a volume of 100 cubic centimeters.
Another Example (with a right triangle):
Say your triangular base has legs of 6 inches and 8 inches (a right triangle), and the prism extends 12 inches:
- Area of triangle = 1/2 × 6 × 8 = 24 in²
- Volume = 24 in² × 12 in = 288 in³
The process never changes. Calculate the triangle area first, then multiply by the prism’s depth or length.
Safety Warning: Make sure you’re measuring the triangle’s height perpendicular to its base, not along a slanted side. This is where most people slip up. If you’re measuring a physical object, use a right angle tool or carpenter’s square to ensure accuracy.
Real-World Examples
Example 1: A Tent
Imagine a camping tent shaped like a triangular prism. The triangular front face has a base of 8 feet and a height of 5 feet. The tent is 12 feet long (front to back).
- Triangle area = 1/2 × 8 × 5 = 20 ft²
- Volume = 20 ft² × 12 ft = 240 ft³
That’s the interior volume—useful if you’re figuring out how much gear fits inside or calculating ventilation needs.
Example 2: A Roof Truss
A roofing contractor needs to estimate materials for a triangular roof section. The triangular end has a base of 30 feet and a peak height of 10 feet. The roof section spans 50 feet along the house.
- Triangle area = 1/2 × 30 × 10 = 150 ft²
- Volume = 150 ft² × 50 ft = 7,500 ft³
This helps estimate insulation, lumber, or ventilation requirements. According to Family Handyman’s construction guides, accurate volume calculations are critical for material budgeting and waste reduction.
Example 3: A Wedge of Cheese or Chocolate
A triangular prism-shaped chocolate bar has a triangular face with a base of 3 cm and height of 2 cm. The bar is 15 cm long.
- Triangle area = 1/2 × 3 × 2 = 3 cm²
- Volume = 3 cm² × 15 cm = 45 cm³
If you know the density of chocolate (about 1.2 g/cm³), you can calculate the weight: 45 × 1.2 = 54 grams.
Example 4: A Water Trough
A triangular water trough for livestock has a triangular cross-section with a base of 2 feet and height of 1.5 feet. It runs 20 feet long.
- Triangle area = 1/2 × 2 × 1.5 = 1.5 ft²
- Volume = 1.5 ft² × 20 ft = 30 ft³
- In gallons: 30 ft³ × 7.48 gallons/ft³ ≈ 224 gallons
This tells you exactly how much water the trough holds—essential for farm planning.
Common Mistakes to Avoid
Mistake 1: Confusing the Triangle Height with the Prism Length
This is the #1 error. The triangle height is the perpendicular distance from the base to the opposite vertex of the triangle. The prism length is how far the prism extends. They’re completely different measurements. Double-check which is which before calculating.
Mistake 2: Forgetting the 1/2 in the Triangle Area Formula
The area of a triangle is always 1/2 × base × height. If you skip the “1/2,” you’ll get twice the correct answer. This cascades into your final volume, so it’s a big deal.
Mistake 3: Using the Wrong Triangle Dimensions
Make sure you’re using the base and height of the triangle, not the lengths of all three sides. If you have a triangle with sides of 5, 6, and 7 cm, you need the perpendicular height from the base, not the side lengths.
Mistake 4: Mixing Units
If your triangle base is in inches and your prism length is in feet, convert everything to the same unit first. Otherwise, your answer will be meaningless. For example, convert feet to inches before multiplying.
Mistake 5: Not Checking If the Triangle Is Right-Angled
If the triangle is a right triangle, you can use the two legs as base and height directly. If it’s not, you must measure or calculate the perpendicular height. Don’t assume.
Pro Tip: Always write down your units at every step. This catches mistakes immediately. “10 cm²” is different from “10 cm,” and your brain will catch the error if you write it out.
Using Tools and Calculators
While you should understand the math, there’s no shame in using tools to verify your work or speed things up.
Spreadsheet Method (Excel or Google Sheets)
You can set up a simple formula. If you’re working with how to add columns in Excel, you can organize your data like this:
- Column A: Triangle base
- Column B: Triangle height
- Column C: Prism length
- Column D: Formula = (A × B / 2) × C
This is especially useful if you’re calculating volumes for multiple prisms. You can also combine cells in Excel to create a nice summary table. For more complex calculations, you might subtract values in Excel to find differences between volumes or compare materials needed.
Online Calculators
Search “triangular prism volume calculator” and you’ll find dozens of free tools. Plug in your numbers and get instant results. These are great for checking homework or quick estimates on a job site.
Mobile Apps
There are geometry calculator apps for iOS and Android that handle 3D shapes. They’re handy if you’re working in the field and need quick calculations.
Geometric Software
If you’re doing professional design work, software like AutoCAD, SketchUp, or Blender can calculate volumes automatically. These tools are overkill for simple prisms but invaluable for complex projects.
The Manual Approach (Best for Learning)
Do the math by hand at least once. You’ll understand the concept better and catch errors more easily. Plus, there’s no battery to die on a job site.
Practice Problems
Ready to test your skills? Try these:
Problem 1: A triangular prism has a triangular base with a base of 7 cm and height of 5 cm. The prism is 12 cm long. What’s the volume?
Answer: (1/2 × 7 × 5) × 12 = 17.5 × 12 = 210 cm³
Problem 2: A tent has a triangular front with a base of 10 feet and height of 6 feet. It’s 15 feet deep. What’s the volume in cubic feet?
Answer: (1/2 × 10 × 6) × 15 = 30 × 15 = 450 ft³
Problem 3: A right triangular prism has legs of 4 inches and 3 inches, with a length of 20 inches. Find the volume.
Answer: (1/2 × 4 × 3) × 20 = 6 × 20 = 120 in³
Problem 4: You have a triangular water channel with a base of 1.5 meters and height of 0.8 meters. It runs for 25 meters. What’s the volume in cubic meters?
Answer: (1/2 × 1.5 × 0.8) × 25 = 0.6 × 25 = 15 m³
Problem 5 (Tricky): A prism has a triangular base with sides of 5, 12, and 13 cm. The prism is 8 cm long. Find the volume. (Hint: This is a right triangle. Which two sides are the base and height?)
Answer: This is a right triangle (5-12-13 is a Pythagorean triple). Base and height are 5 and 12. Volume = (1/2 × 5 × 12) × 8 = 30 × 8 = 240 cm³
According to This Old House’s building and construction articles, understanding volume calculations is essential for any DIY or professional project. Getting the math right saves money and prevents material waste.
Frequently Asked Questions
What’s the difference between a triangular prism and a triangular pyramid?
– A triangular prism has two parallel triangular bases and three rectangular sides. A triangular pyramid (tetrahedron) has one triangular base and three triangular sides meeting at a point. The pyramid is pointy; the prism is flat on both ends. Their volume formulas are different: prism = base area × length, while pyramid = (1/3) × base area × height.
Can I use this formula for any triangle, or just right triangles?
– Yes, this formula works for any triangle—right, acute, or obtuse. As long as you use the correct perpendicular height (not a slanted side), the formula applies. If you have a non-right triangle, you might need to measure or calculate the perpendicular height carefully.
What if I only know the three side lengths of the triangle, not the height?
– You can use Heron’s formula to find the area first. If the sides are a, b, and c, calculate the semi-perimeter s = (a + b + c) / 2, then area = √[s(s-a)(s-b)(s-c)]. Once you have the area, multiply by the prism length. It’s more work, but it works.
How do I convert cubic centimeters to liters?
– Divide by 1,000. One liter = 1,000 cm³. So 5,000 cm³ = 5 liters. This is useful for calculating tank volumes or liquid capacity.
What if the prism is tilted or slanted instead of straight?
– If the prism is oblique (slanted), the formula still works as long as you measure the perpendicular distance between the two triangular bases, not along the slanted edges. The volume doesn’t change just because it’s tilted.
Can I calculate the volume if I only know the surface area?
– No, not without additional information. Surface area and volume are related but separate properties. You need actual dimensions (base, height, length) to calculate volume.
Why is the triangle area formula 1/2 × base × height?
– A triangle is half of a rectangle. If you have a rectangle with base b and height h, its area is b × h. A triangle with the same base and height takes up exactly half that space, so the area is 1/2 × b × h. This is why the factor of 1/2 appears.
How accurate do my measurements need to be?
– It depends on the application. For homework, being within 1-2% is fine. For construction or engineering, you might need precision to 1/16 inch or better. Use appropriate measuring tools: a ruler for small objects, a tape measure for larger ones, and calipers for precise dimensions.
What’s the difference between volume and capacity?
– Volume is the amount of space an object occupies. Capacity is how much a container can hold. For a solid prism, they’re the same number (though the units might differ: cm³ vs. milliliters). For a hollow container, capacity might be slightly less than the outer volume.
Can I use this formula for a prism with an irregular triangle?
– Yes, as long as it’s a flat triangle with straight edges. Irregular just means the sides aren’t equal or the angles aren’t all the same. Calculate the area of your irregular triangle (perpendicular base × height ÷ 2), then multiply by the prism length.
For additional resources on geometry and measurements, check out OSHA’s workplace safety guidelines, which include standards for measuring and calculating volumes in industrial settings. And Bob Vila’s home improvement guides offer practical applications for volume calculations in DIY projects.
Final Thoughts
Learning how to find the volume of a triangular prism is genuinely useful. Whether you’re a student, a contractor, or just curious about geometry, this skill applies to real situations: estimating tent space, calculating roof materials, or figuring out how much liquid a container holds.

The formula is simple: find the triangular base area, then multiply by the prism’s length. The hard part is measuring accurately and avoiding the common mistakes we discussed. Take your time, double-check your units, and don’t skip the 1/2 in the triangle area formula.
Practice with the problems above, and you’ll build confidence quickly. And remember: geometry isn’t abstract—it’s all around you. Every tent, roof, wedge, and channel is a real-world application of this formula.